著者:ptr-yudai(@ptrYudai)
はじめに
5月27日から29日にかけて、世界最大のハッキングコンテストDEF CONの予選CTFが開催されました。48時間の制限時間で、世界中から参加した535チームのうち、上位11チームのみが決勝に進めるという、去年よりもさらに厳しい競技となりました。
リチェルカセキュリティの社員・アルバイトには、現役でCTFに取り組んでいるメンバーが多数在籍しています。CTFは多種多様な前提、制約、技術領域に触れる機会になり、業務の実行能力向上にも繋がります。そこで、去年に引き続き、会社としてDEF CONに挑戦することにしました。
弊社にはTokyoWesternsやbinjaなどをはじめとして、複数の強豪チームのメンバーが在籍しています。今回も、各チームのメンバーにも協力をいただき、合同チーム「undef1ned」として出場しました。
 |
| 競技中の食事やお菓子も支援してもらいました |
結果、今年は世界中から500を超えるチームが参加し、我々は世界11位(日本国内1位)で決勝へと歩を進めることができました🎉
 |
| 昨年より厳しい条件の中、無事予選を突破 |
ziggypop
今年も数多くの難問が出題されました。この記事では、その中でも点数が高かった「ziggypop」という問題のwriteupを公開しようと思います。
この問題は、Zig言語で作られたサーバーを解析するReversingの問題です。弊社では過去にさまざまな言語でさまざまなアーキテクチャ向けに作られたバイナリを解析した経験があります。特に著者のptr-yudaiは過去にZig言語製のプログラムを解析した経験があったため、この問題に取り組み始めました。参加した弊社メンバーからは、アルバイトのkeymoonさん、moratorium08さん、そして正社員のptr-yudaiがこの問題に主に取り組みました。
問題概要
この問題ではmainという名前のx86-64向けのELFファイルが配布されます。
$ file main
main: ELF 64-bit LSB pie executable, x86-64, version 1 (SYSV), static-pie linked, stripped
エントリーポイントの関数のControl Flow Graphを見ると、次のようにぐちゃぐちゃな見た目をしています。
 |
| エントリーポイントのCFG |
これだけでなく、他にも呼ばれている関数がたくさんありますが、根気よく1つずつ解析していきましょう。
プログラムの実行
まず、straceで挙動を調べると、プログラムはサーバーとして接続を待ち受けていることがわかります。
$ strace ./main
execve("./main", ["./main"], 0x7ffca46f9820 /* 72 vars */) = 0
arch_prctl(ARCH_SET_FS, 0x7fc5e4bdd028) = 0
prlimit64(0, RLIMIT_STACK, {rlim_cur=16384*1024, rlim_max=16384*1024}, NULL) = 0
socket(AF_INET, SOCK_STREAM|SOCK_CLOEXEC, IPPROTO_TCP) = 3
setsockopt(3, SOL_SOCKET, SO_REUSEADDR, [1], 4) = 0
bind(3, {sa_family=AF_INET, sin_port=htons(8675), sin_addr=inet_addr("0.0.0.0")}, 16) = 0
listen(3, 128) = 0
getsockname(3, {sa_family=AF_INET, sin_port=htons(8675), sin_addr=inet_addr("0.0.0.0")}, [16]) = 0
mmap(NULL, 4096, PROT_READ|PROT_WRITE, MAP_PRIVATE|MAP_ANONYMOUS, -1, 0) = 0x7fc5e4bdb000
accept4(3,
しかし、ncで接続してもすぐにクラッシュしてしまいます。
[ 4349.293387] traps: main[11844] trap invalid opcode ip:7fc307edc016 sp:7ffd8fc922b8 error:0 in main[7fc307ed1000+c000]
gdbで見ると次の箇所で停止します。
pwndbg> x/4i 0x7ffff7ff8016
=> 0x7ffff7ff8016: vprold xmm2,xmm1,0x18
0x7ffff7ff801d: vprold xmm3,xmm4,0x9
0x7ffff7ff8024: vpand xmm1,xmm2,xmm3
0x7ffff7ff8028: vpslld xmm1,xmm1,0x3
実は今回のプログラムはIntelのAVX-512という拡張命令セットを利用しています。残念ながら、私のマシンは一部の命令に対応していなかったため、Illegal Instructionでプログラムが落ちてしまいました。
アルバイトの方のマシンでは正常に動作することが終盤でわかりましたが、いずれにせよ動作確認のたびに他の人に実行を依頼していては埒が明きません。まずは自分のマシンで動作させる方法を考えました。
まっさきに思いついたのが**Intel SDE**(Software Development Emulator)です。SDEは名前の通りエミュレータで、Intel命令セットのプログラムをエミュレートしてくれます。内部的にはIntel PINを使っており、新しい命令セットの再現や実行トレースの取得もできます。
$ ./sde64 -skx -- ./main
上記コマンドではSkylake server CPUを選択して実行しました。ncで接続してみます。
$ nc localhost 8675 | hexdump -C
00000000 c2 9f f0 76 3b ab b9 8f a6 19 ef f0 76 a6 d2 e1 |...v;.......v...|
00000010 cb 1d 48 b1 fc a0 f1 89 f4 0f 0b be 50 d1 f6 73 |..H.........P..s|
応答がありました!これで無事プログラムを実行できます。
プログラムの動的解析
実行はできましたが、SDEの上で動いているため、このままではgdbでデバッグできません。SDEにはgdbでアタッチできる機能もありますが、非常に動作が遅いため、なるべく避けて通りたいです。
今回問題を解き進める上で、「ある時点でのメモリとレジスタの状態を確認したい」という需要がありました。ステップ実行のような贅沢な機能は諦めても、最低限ブレークポイントが必要であると判断しました。
そこで、Intel PINの性質を使って簡易的なブレークポイントを再現することにしました。PINは命令をフェッチし、トレース単位でJITコンパイルします。これにより、例えばさきほどクラッシュを引き起こしていた vprold 命令は、実行中のCPUがサポートする別の命令列に置き換えられます。実行可能な命令は通常そのままの形で登場するため、使われるレジスタも同じになります。
したがって、実行を停止したい箇所に、中身を知りたいレジスタを使ってSIGSEGVを引き起こす命令を設置すれば、そのレジスタの状態を持ったままクラッシュします。競技中はこのクラッシュによる停止を使ってデバッグしました。CTFのように速さが求められる作業では、このように雑でも使える方法が解析に役立ちます。
次のコードはアドレス0x36dcでプログラムを停止させ、 rsp の値を調べる際に使ったパッチです。
from ptrlib import *
data = assemble("xor eax, eax; mov [rax], rsp;")
addr = 0x36dc
with open("./main", "rb") as f:
buf = f.read()
buf = buf[:addr-0x1000] + data + buf[addr-0x1000+len(data):]
with open("./patched", "wb") as f:
f.write(buf)
import os
os.system("chmod +x patched")
プログラムの静的解析
ここからが最も重たい部分です。プログラムの処理を解析して、フラグを手に入れる方法を調べましょう。
すでに対象プログラムがfork型サーバーとして動作していることを知っているので、 accept fork の後の処理を探します。まず accept が一箇所あるので、その周辺を調べます。
 |
| 接続を受け付けるコードの周辺 |
accept の後には sub_401B が呼ばれていますが、これは明らかに fork です。
 |
| 接続を受け付けるとforkする |
Zig製のバイナリを読んでいるとすぐに気づきますが、下図のように、Zigの変数はポインタとサイズの組で表現されます。
 |
| Zigにおけるメモリ上での変数の表現 |
例えば以下の関数 sub_3FFE を見てみましょう。
 |
| Zigの変数を引数に取る関数呼び出しの例 |
中身は次のようになっています。 v2 には第二引数の変数サイズが入るので、第一引数の変数バッファに第二引数の変数バッファをコピーしていることが分かります。
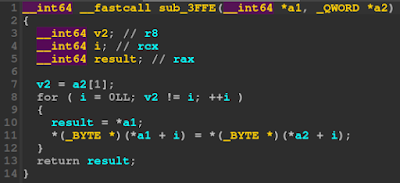 |
| Zigの変数を扱う関数の例 |
このように、まずは対象の言語が変数や定数をメモリ上でどのように表現しているかや、関数の呼び出し規約などを知っておくことで、解析しやすくなります。
さて、しばらく読み進めると sub_9EB6 ( sub_AC54 のラッパ)と sub_9EBB ( sub_AAD5 のラッパ)という2つの関数が登場します。内部ではシステムコールが呼ばれています。 sub_9EB6 はrax=1なので write 、 sub_9EBB は read であることが分かります。
 |
| write関数 |
 |
| read関数 |
ncで接続したときに毎回ランダムな32バイトの値が出力されていました。これがこの write 呼び出しに該当すると思われます。このデータの意味がわかるまでは、この32バイトの値を乱数Xと呼ぶことにします。
 |
| ncで表示される乱数を出力している箇所 |
IDAはSIMD命令に弱いので上図のような残念なデコンパイル結果になっていますが、読んでいきましょう。デコンパイル結果中の変数はほとんど意味のないものになっているため、適宜アセンブリコードと比較しながら読み進めます。
さて、乱数Xの出力サイズは0x20バイト固定で、データポインタは rsp+0x400 から来ています。このデータの元をたどると、非常に煩雑なコードを経て生成されているデータであることが分かります。特に序盤では sub_4159 がひどく、とてもではありませんが読めるような見た目をしていません。
 |
| 人間が読むには複雑なコードが出力されている |
一番最初に乱数Xが使われる箇所は sub_4057 です。この関数の中では0x20バイトの乱数が生成されます。乱数は sub_CD1A で作られ、ここでは getrandom システムコールを使って安全な乱数を生成しています。
 |
| 乱数Xのソースはgetrandomシステムコール |
生成される乱数と送られる乱数Xは異なるものなので、 sub_4057 で作られた乱数を sub_4159 や write 前のSIMD命令などを通して変形してから送信しているものと思われます。これらの関数を読むのは大変なので、一度後回しにして入力 read 以降を読み進めていきましょう。
read では32バイトのデータを入力します。このデータに対してたくさんのSIMD命令を適用した後、次の条件分岐があります。条件が成立しないとプログラムは終了します。したがって、最初の関門はここを通過できる入力を探すことです。
 |
| 最初の入力をチェックする箇所 |
どうやらこれまで無視してきていたSIMD命令や、複雑な関数を調べる必要がありそうです。
Reversingにおいて複雑な関数を調査するとき、まずは既存のコードを調べるのが好手になりやすいです。今回はまず、比較的簡単な見た目をしている sub_0D7F を調べることにしました。
 |
| 特徴的な定数から該当するアルゴリズムを調べる |
図のように、 bzhi 命令(レジスタの特定のビットより上位を取り出す命令)を多用しています。また、途中で51ビットのシフトがたくさん登場することや、0x7FFFFFFFFFFEDという値を足していることも特徴的です。そこで、「51 0x7FFFFFFFFFFED」で検索すると、 boringssl というリポジトリの curve25519_64.h がヒットします。
https://boringssl.googlesource.com/boringssl/+/master/third_party/fiat/curve25519_64.h
static FIAT_25519_FIAT_INLINE void fiat_25519_subborrowx_u51(uint64_t* out1, fiat_25519_uint1* out2, fiat_25519_uint1 arg1, uint64_t arg2, uint64_t arg3) {
int64_t x1;
fiat_25519_int1 x2;
uint64_t x3;
x1 = ((int64_t)(arg2 - (int64_t)arg1) - (int64_t)arg3);
x2 = (fiat_25519_int1)(x1 >> 51);
x3 = (x1 & UINT64_C(0x7ffffffffffff));
*out1 = x3;
*out2 = (fiat_25519_uint1)(0x0 - x2);
}
...
fiat_25519_subborrowx_u51(&x1, &x2, 0x0, (arg1[0]), UINT64_C(0x7ffffffffffed));
fiat_25519_subborrowx_u51(&x3, &x4, x2, (arg1[1]), UINT64_C(0x7ffffffffffff));
fiat_25519_subborrowx_u51(&x5, &x6, x4, (arg1[2]), UINT64_C(0x7ffffffffffff));
fiat_25519_subborrowx_u51(&x7, &x8, x6, (arg1[3]), UINT64_C(0x7ffffffffffff));
fiat_25519_subborrowx_u51(&x9, &x10, x8, (arg1[4]), UINT64_C(0x7ffffffffffff));
sub_0D7F にかなり近い見た目をしています!つまり、これまでわからなかった謎のSIMD命令は、楕円曲線演算に関わる命令なのではないかと予測できます。
ZigでCurve25519を扱うライブラリを探すと、標準ライブラリがありました。
https://github.com/ziglang/zig/blob/master/lib/std/crypto/25519/curve25519.zig
このコードと機械語を照らし合わせることで、点のスカラー倍やバイト列へのエクスポートなど、これまで無視してきた関数の中身がわかりはじめました。
ここまで判明している内容を擬似コードに落とすと、次のようになります。
u8 secret[0x20], Q_bytes[0x20];
GetRandom(secret, 0x20);
Curve25519 P;
P = secret * G; // Gは固定のベースポイント
// PA=sA*Gを送ってPB=sB*Gを受け取る
write(sock, P.toBytes(), 0x20);
read(sock, Q_bytes, 0x20);
Curve25519 Q(Q_bytes);
// 共有鍵
Curve25519 abG = secret * Q;
assert (abG.limbs[0] & 0xffff000000 == 0xc0aa000000);
楕円曲線Diffie-Hellman鍵共有を実装していますが、こちらから送る点は特徴的な点でないと受け付けてくれません。 limbs はCurve25519における点の圧縮表現で、この最初のデータの上位16ビットを0xc0aaと比較しています。数学的な意味があるのかはわかりませんが、16ビットなので適当な点を生成して、条件を満たすものを選択すれば総当りでも良さそうです。
PA = sock.recvonce(0x20)
print(PA)
while True:
sB = random_int(1, (1<<256)-1)
abG = mul_P(sB, PA)
if (to_x(abG)[0] & 0xffff000000) == 0xc0aa000000:
logger.info(f"Found valid secret: 0x{sB:x}")
break
PB = mul_G(sB)
sock.send(PB) # sB * G
logger.info("PB: " + PB.hex())
logger.info("abG: " + abG.hex())
これで条件を満たす点を渡し、鍵共有に成功しました。
では、続きを読んでいきましょう。
 |
| ECDH鍵共有成功後のコード |
また新しい関数が登場しました。今度は点15のバイト表現を受け取って処理をしていますが、該当する関数はZigのCurve25519には見つかりません。
これらの関数も複雑なロジックなので、マジックナンバーやCFGの形などを元に調査してみます。まずは一番多く呼ばれている sub_A016 を調べてみます。中では次のような複雑な関数を呼んでいます。
 |
| 特徴的な定数から該当するアルゴリズムを調べる その2 |
登場する数値の1つとして「0x428A2F98」を選んで検索してみると、SHA-256がヒットします。はじめは単にSHA-256を計算しているのかと思いましたが、ところどころ説明のつかない機械語が登場します。同様の値が使われるBLAKE系のハッシュも調査しましたが、ここでしばらく考えました。
しばらくすると、チームメンバーからSHA-256をHMACとして使っているのではないかという予想が挙がりました。上記ハッシュの後に、次のようなループ処理があります。
 |
| PBKDF2にみられるループ |
暗号に強いメンバーからPBKDF2に見えるという意見があり、実際にコードを見てもかなり近い見た目をしていることがわかります。
徐々にPBKDF2-SHA256であることが明らかになってきました。ループ中に登場する
3 * v139 + 21
という計算が本来存在しない処理なので疑問でしたが、暗号要員にそこだけ追加して再現してもらうと、デバッグ時と値が一致することが判明しました。
ここまでで、楕円曲線DH鍵共有で共有した点をバイト表現としてPBKDF2に渡し、その結果を共通鍵として利用していることが分かりました。新たに判明した場所の疑似コードは次のようになります。
// PBKDF2-SHA256の改造版
SHA256 ctx = Prf.init(abG.toBytes()); /* rsp+0x1900 */
ctx.update(abG);
ctx.update(0x10000000.toBytes("big endian"));
ctx.final(prev_block);
dk_block = prev_block; // memory copy
for (int rounds = 1; rounds < 1000; rounds++) {
SHA256 ctx2 = Prf.init(abG.toBytes()); /* rsp+0x700 */
ctx2.update(prev_block);
ctx2.final(secret);
prev_block = new_block; // memory copy
u32 val = 0;
for (int j = 0; j < 32; j++) {
dk_block[j] ^= prev_block[j];
val = rounds + ((3 * prev_block[j] + 21) ^ val) % 0xffffff;
}
}
ここまで解析してもまだフラグが見えませんが、次が最後の山場です。
まず、0x18バイトのデータと、0x110バイトのデータを受け付けます。
 |
| 最後のユーザー入力 |
少し読み飛ばすと、次のようにフラグを開いている箇所が見つかります。
 |
| フラグと思われるファイルを開いている箇所 |
さらに続いて write が呼ばれていることから、送ったデータの正当性を検証してフラグを出力するか、送ったデータに基づいてフラグを暗号化して出力するか、フラグに関するデータを出力する処理があると考えられます。
ここで登場する処理も新しい関数なので、調査していきましょう。例えば sub_A329 を見ると、次のように計算処理があります。XORが多いことから、数値計算というよりハッシュ関数や暗号のような計算に見えます。
 |
| ハッシュ関数や暗号アルゴリズムのようなアセンブリ |
この関数の冒頭では sub_AECC を呼び出しており、そこでは xmmword_BC0 が参照されています。このアドレスは定数領域で、次のようなデータが入っています。
 |
| 特徴的な定数から該当するアルゴリズムを調べる その3 |
この値はASCIIで expand 32-byte k であり、ChaChaやSalsa20で使われるマジックナンバーです。アセンブリとZigの実装を読み比べると、XSalsa20に近いことが判明しました。さらに、CFGの形やZigの変数の呼び出し規約などと照らし合わせると、XSalsa20Poly1305と酷似していることがわかります。
したがって、鍵共有後の最初の read で0x18バイトのnonceを受け取っていたことになります。Salsaの鍵としてPBKDF2-SHA256で共有した鍵が使われます。もう1つの read で送った0x110バイトのうち、最初の0x10バイトはtagを表しており、残りの0x100バイトがデータを復号します。復号した結果は次の箇所で使われています。
 |
| 復号結果の検証コード |
復号結果の最初のバイトが0x02かどうかを確認しています。楕円曲線の点のチェックもそうでしたが、意味のあるチェックというより、プログラムを理解しているかのためのチェックのようです。ここまでを疑似コードで表してみます。
read(sock, nonce, 0x18);
read(sock, nazo2, 0x110);
u8 data[0x40];
MemoryCopy(data, b"\\x00"*0x20 + nazo2[0x10:0x30]);
XSalsa20Poly1305 s = XSalsa20Poly1305(dk, nonce);
data = s.decrypt(data, nazo2[0:0x10], "", nonce, dk);
assert (data[0] == 2);
上記のチェックを完了したら、フラグがXSalsa20Poly1305で暗号化されて送られてきます。その後に入力と同じ形式で、nonceとtag, 暗号文が送られてきます。
 |
| 暗号化したフラグの送信コード |
疑似コードで表すと次のようになります。
u8 flag[0x100];
int fd = open("flag.txt", O_RDONLY);
read(fd, flag, 0x100);
close(fd);
u8 rnd[0x18];
GetRandom(rnd, 0x18);
XSalsa20Poly1305 s = XSalsa20Poly1305(dk, rnd);
data, tag = s.encrypt(data, "", rnd, dk);
write(sock, rnd, 0x18);
write(sock, tag + data, 0x110);
鍵は共有した鍵が使われているので、ここまでの情報で復号できます。
shared_key = abG
kd = pbkdf2_modified(shared_key, shared_key, 1000)
logger.info("kd: " + kd.hex())
dummy_tag = b'\\x00' * 0x10
while True:
nonce = os.urandom(0x18)
msg = os.urandom(0x100)
m = decrypt(msg, dummy_tag, nonce, kd) # XSalsa20Poly1305
if m[0] == 2:
c, tag = encrypt(m, nonce, kd)
logger.info(" c: " + c.hex())
logger.info(" m: " + m.hex())
logger.info("tag: " + tag.hex())
break
sock.send(nonce)
sock.send(craft_msg(tag, msg))
time.sleep(5)
print("sorosoro...")
nonce = sock.recvonce(0x18)
logger.info("nonce: " + nonce.hex())
tag = sock.recvonce(0x10)
enc = sock.recvonce(0x100)
logger.info("tag: " + tag.hex())
logger.info("enc: " + enc.hex())
flag = decrypt(enc, tag, nonce, kd) # XSalsa20Poly1305
print(flag)
おわりに
長いwriteupになってしまいましたが、競技中も取り組み始めてからフラグが出るまでに17時間をかけて解きました。(LiveCTFや他の問題も担当していたため17時間ずっとこの問題に取り組んでいたわけではありませんが、著者が一番時間を割いた問題であることは間違いありません。)楕円曲線DH鍵共有、PBKDF2、SHA256、XSalsa20Poly1305と、さまざまな暗号やハッシュ関数が詰め込まれており、それらをZigでコンパイルされたコードとして読む必要があるため非常に大変な問題でした。
CTF・業務問わず、リバースエンジニアリングという作業は解析者の技術だけでなく、根気も重要になってきます。長時間の解析は体力が物を言うので、今回のDEF CON CTFを通してリバースエンジニアリング能力の向上をまた1つ実感できました。
また、今回の問題は暗号やマイナー言語に強いチームメンバーの力も借りて解くことができ、協力して初めて解ける問題はチーム戦ならではの醍醐味だと感じました。
決勝大会は今年もラスベガスで開催されます。リチェルカセキュリティでは、今回参加してくださった社員・アルバイトの方が決勝大会やDEF CONカンファレンスに参加できるよう、旅費を支援する予定です。
今年もDEF CON CTFに参加してくださった社員、アルバイトの方々、そして協力してくださったチームのメンバーの方々、ありがとうございました!決勝でお会いしましょう👋